Black-Scholes公式模拟期权
期权数据获取
通过Tushare获取所有华夏上证50ETF期权数据。选取17年09月执行价2.30看涨期权，编码‘10000844.SH’。得到执行价、期权到期日、期权有效期等信息。
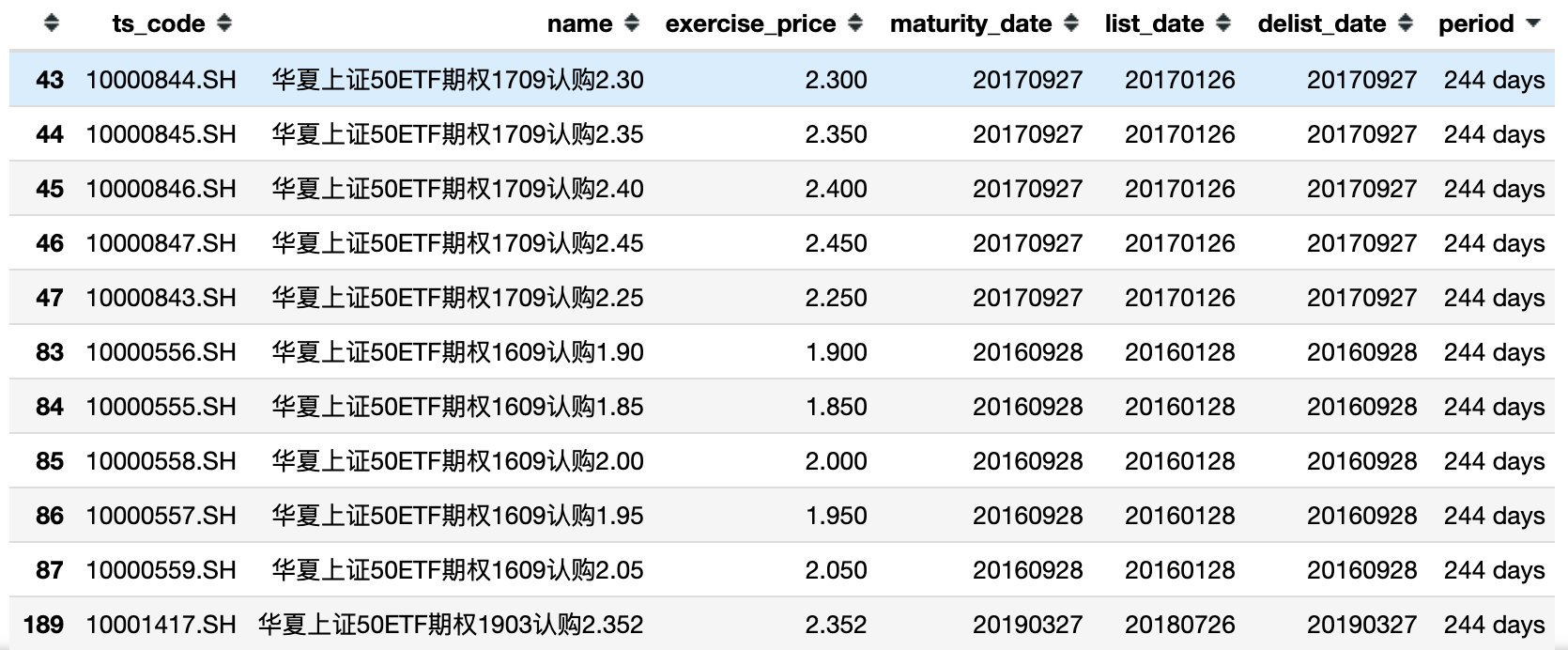
期权交易数据获取
通过Tushare获取17年09月执行价2.30看涨期权，所有交易日的日数据。以该期权每日收盘价为纵坐标，日期为横坐标作图，得到该期权交易变化曲线。
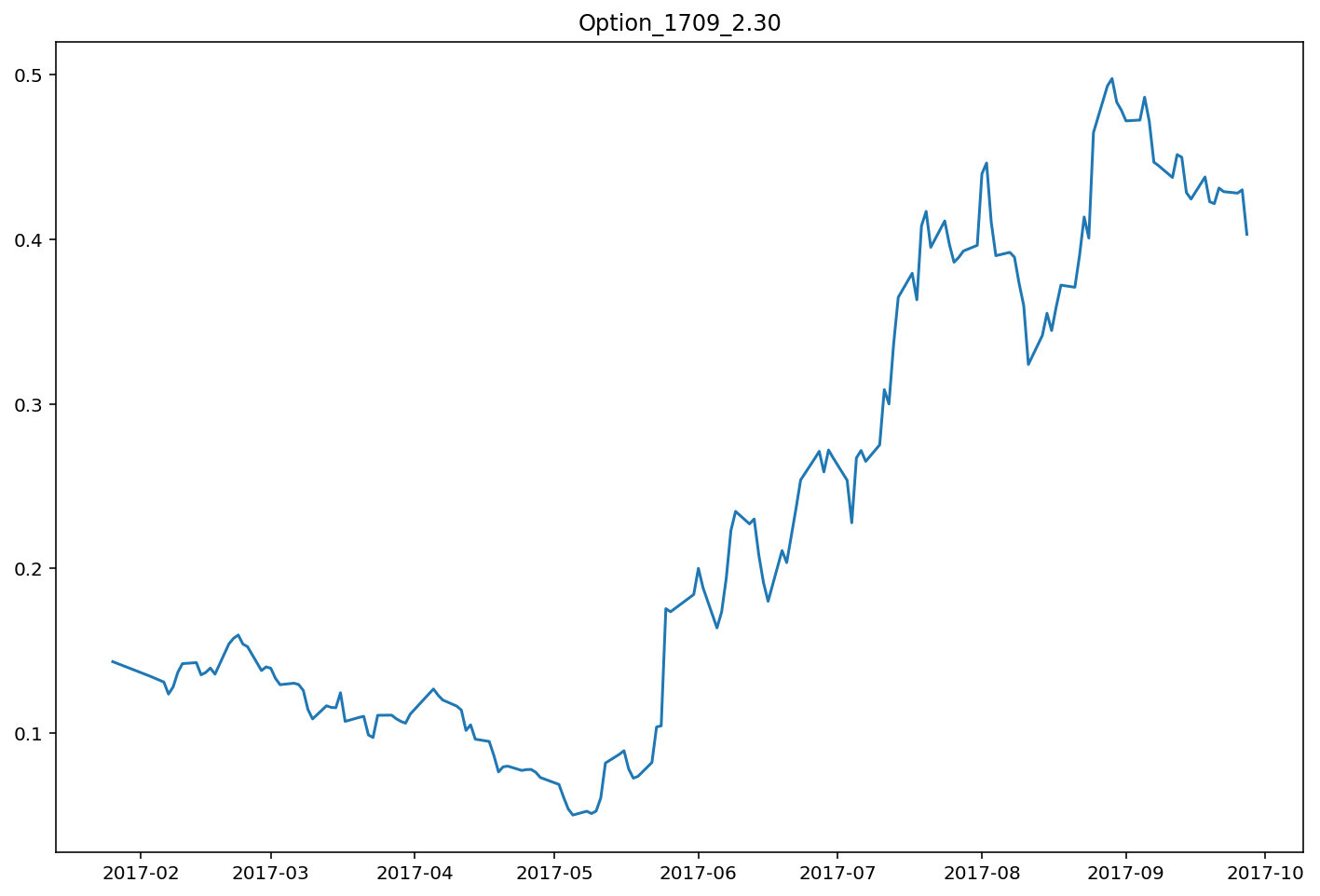
标的资产（ETF50基金）交易数据获取
通过Tushare，获取标的资产 ETFF50的每日交易数日（日期为如上所提期权的有效期及其前300天）。以该基金每日收盘价为纵坐标，日期为横坐标作图，得到该基金交易变化曲线。
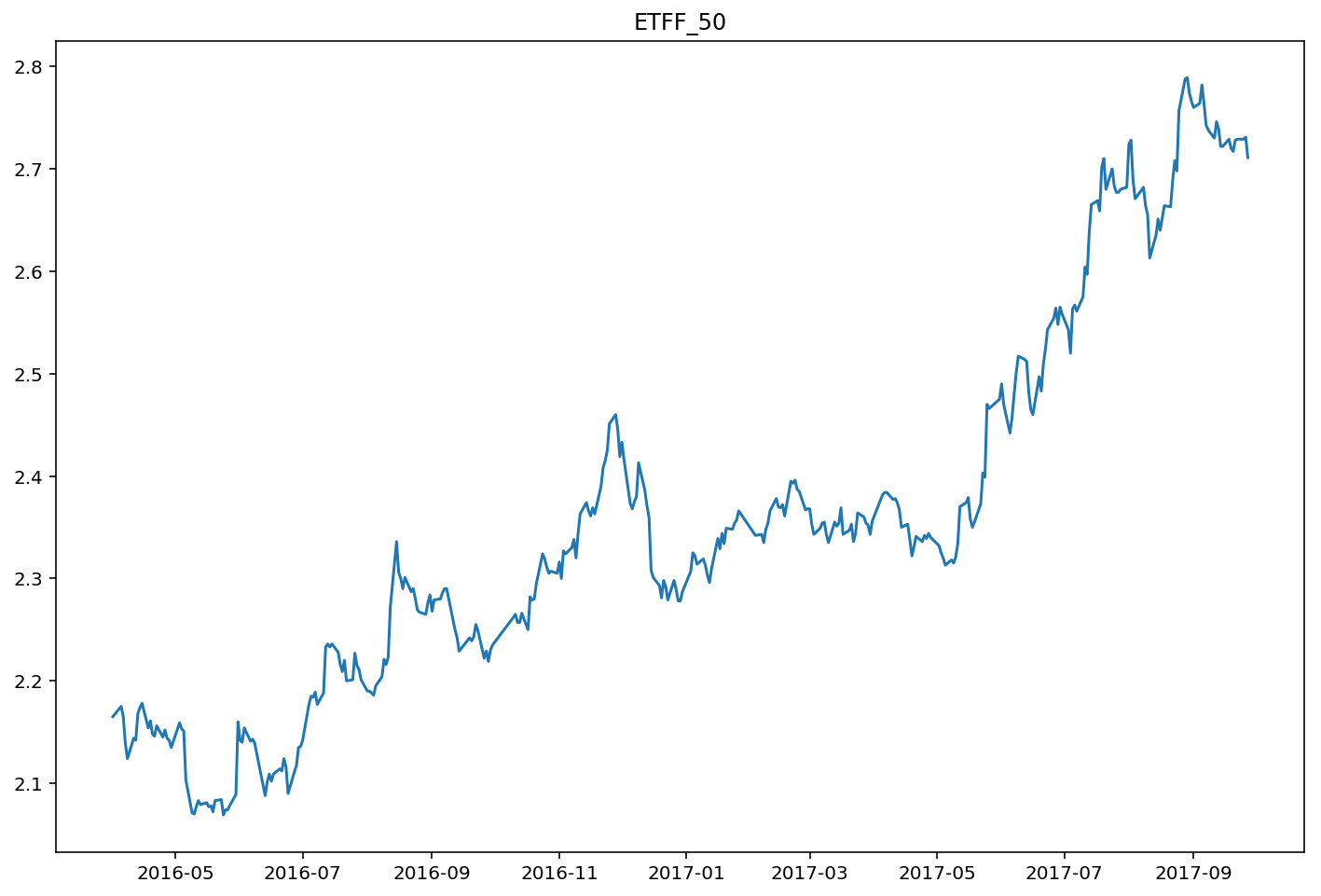
历史波动率（过去30天收益率的年化标准差）计算
得到ETF50日交易记录后，计算日收益率(log return)，并选取30天为移动窗口，计算标准差，并进行年化处理，得到历史波动率。
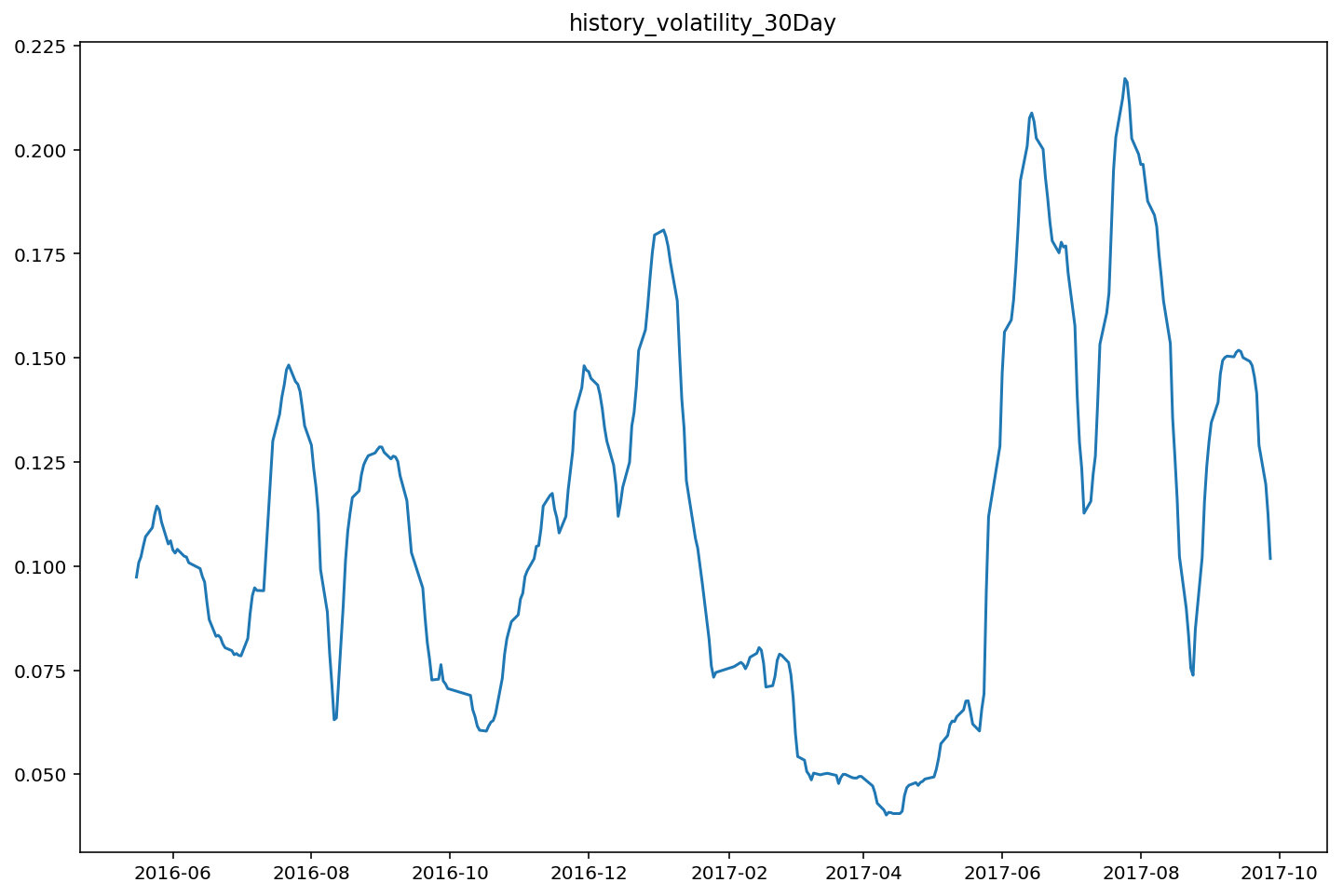
无风险利率（Shibor）数据获取
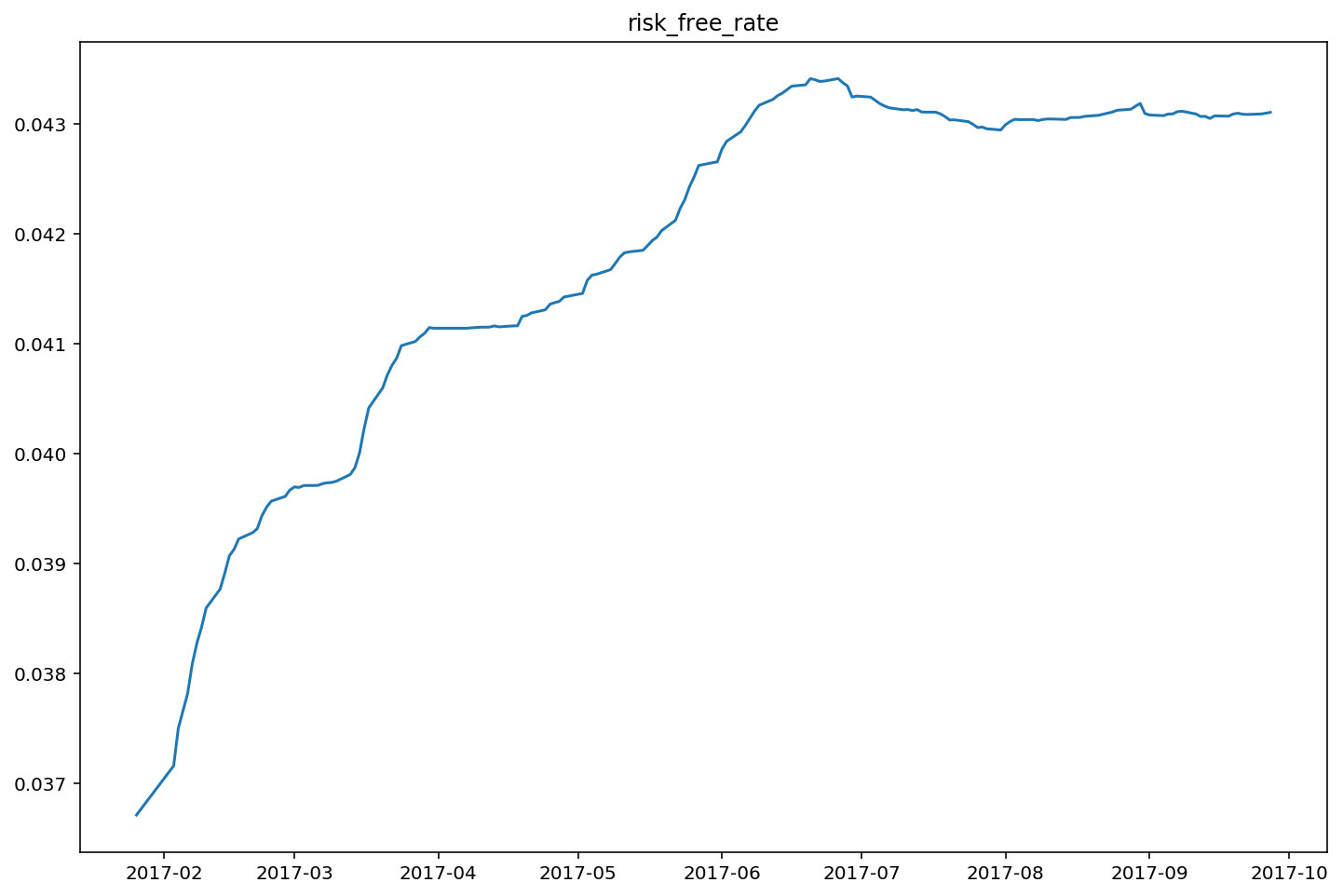
通过Tushare，获取所需期权交易期内，Shibor的利率数据，并转化成连续复利形式。绘制无风险利率曲线。
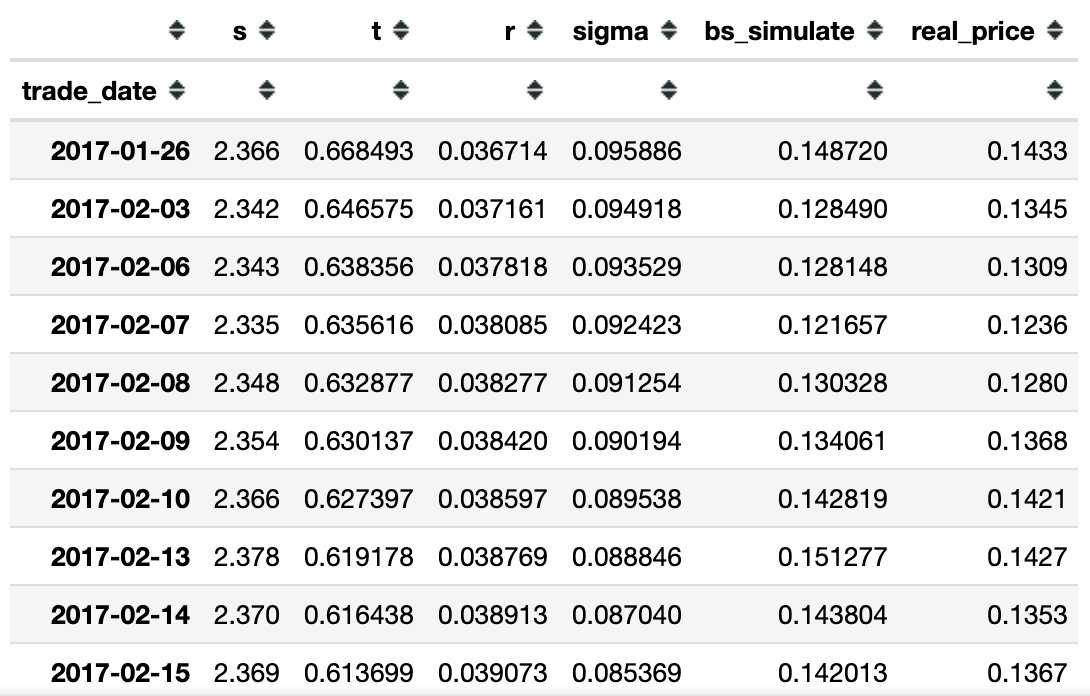
根据Black-Sholes计算期权理论价格
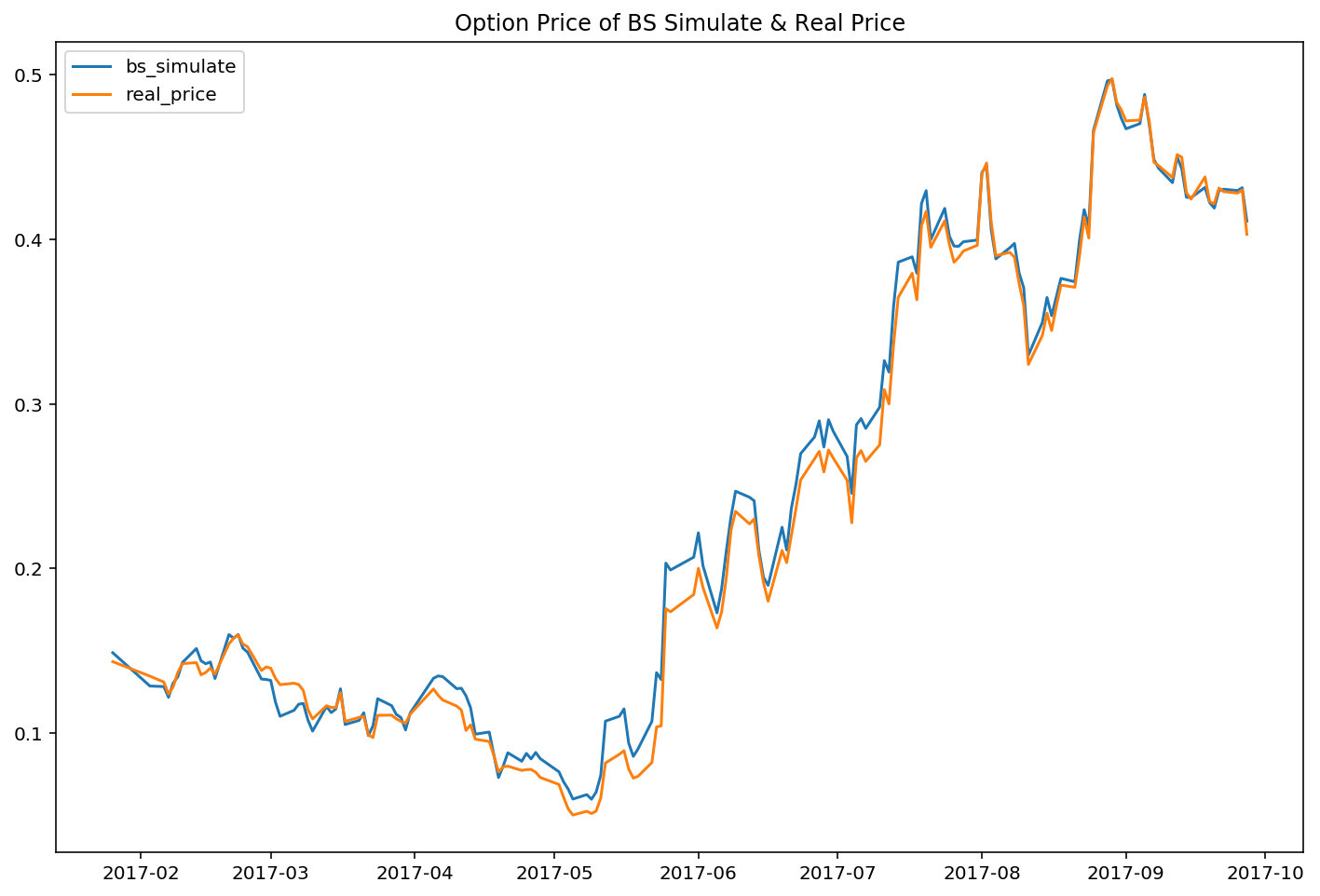
建立Black-Sholes模型，代入上一步中所获取的参数，计算得到期权的理论价格，并绘制曲线，与期权实际价格进行比较。
重复以上步骤，对2018年三月份六月份九月份十二月份，每个月份各选取一只期权进行BS模拟，对比如下图
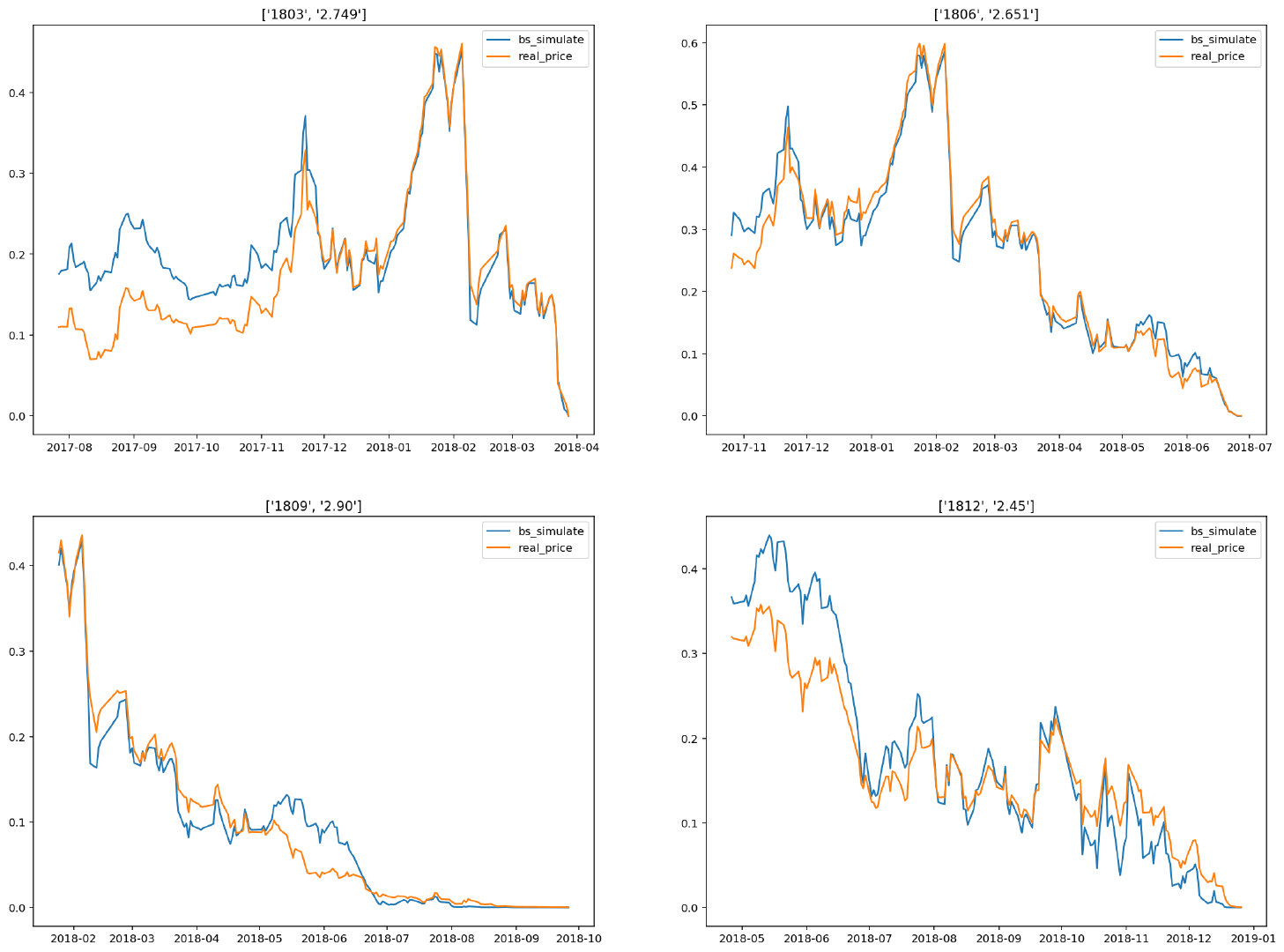
由以上五次模拟图可以看出，BS模拟的价格和真实的价格差距很小。另外，2018年数据比2017年更加难以模拟，特别是第一季度和第四季度，原因是2018年中美贸易战和A股股灾严重影响了市场，使得市场不稳定，模型稍微和实际结果有偏离。
Black-Scholes优化，考虑红利
在考虑红利之后，通过Tushare，获取了ETF50基金的分红数据，如下。
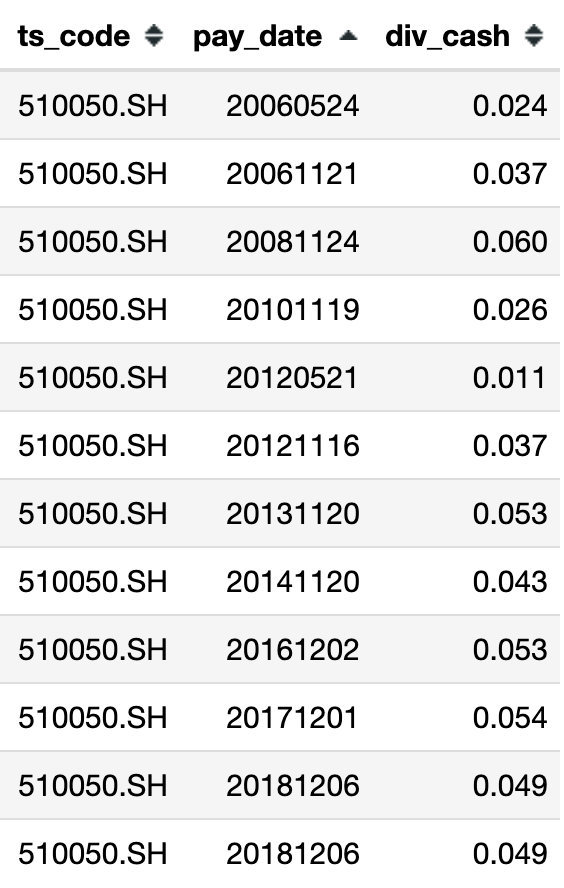
ETF50每年年末进行分红，我们取2018年每股分红0.05元。
绘制了不考虑红利的原始BS模型及考虑了红利的BS模型的模拟结果和真实价格的对比，如下图所示。
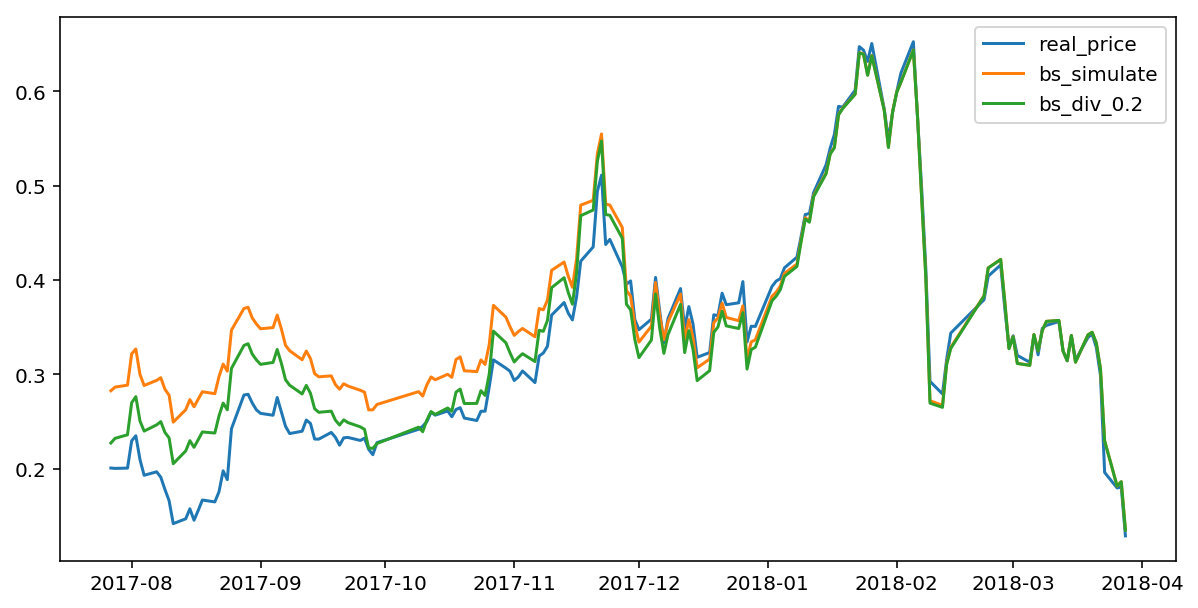
由图可以看出，经过红利修正过的BS模型所模拟出来的价格，比原始BS模型，更加接近真实价格。
波动率修正
在Black-Schole公式中，输入的五个参数，除了波动率外，都是固定且不可改变的：基础资产的价格、无风险利率由市场决定；期权的执行价、有效期由期权合约本身决定。故，要想通过Black-Schole方程获得最为理想的理论价格，”波动率”参数最为重要。
历史波动率
历史波动率是最为广泛使用的波动率，即一段时间内的资产价格收益率（log return）的年化标准差。
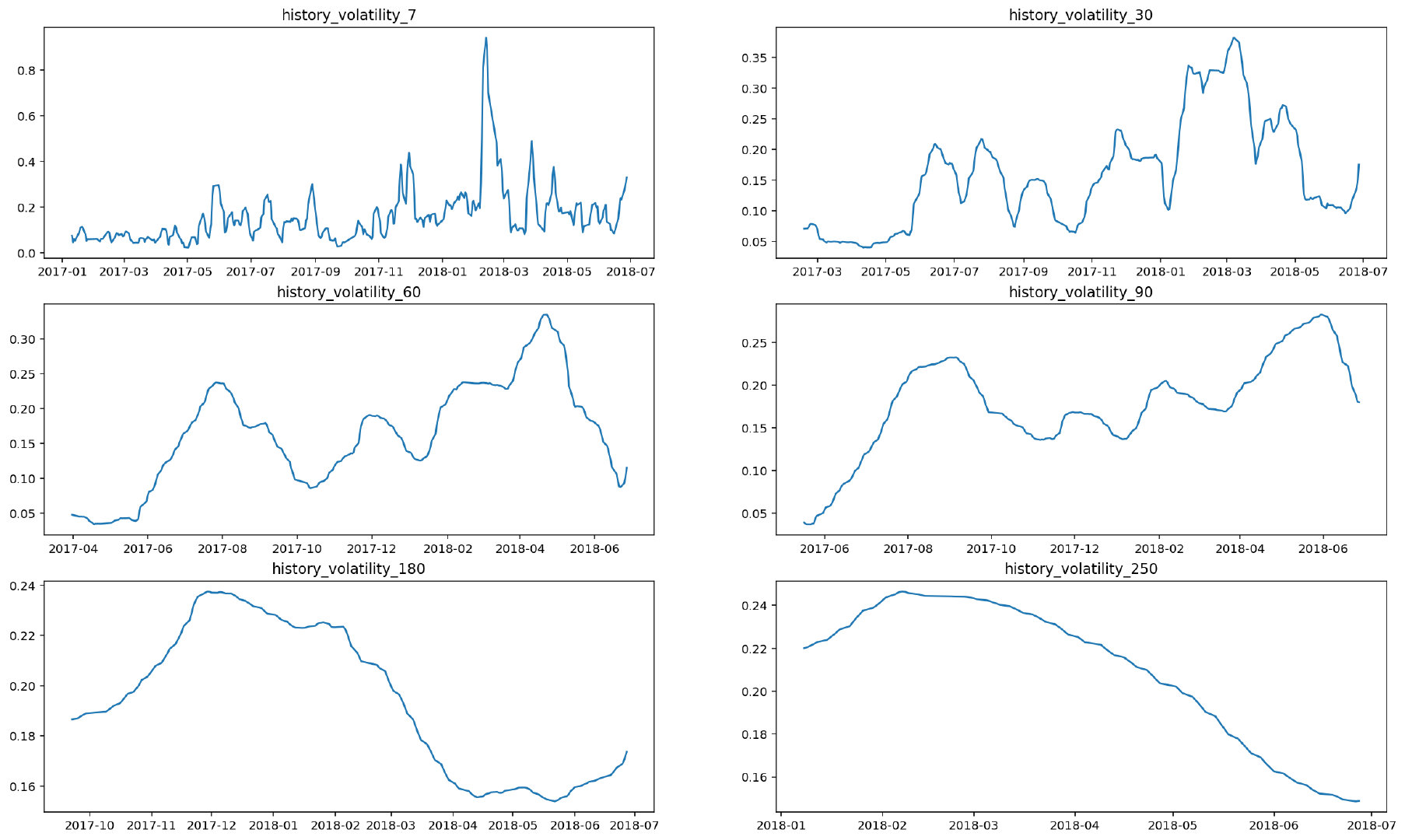
如上图，做出的关于标的资产ETF50的7、30、60、90、180、150天的历史波动率对比图。
7天的历史波动率波动较大，拥有较多噪音；而150天的波动率太过平缓，丢失太多信息。
如何去评判波动率的方法优劣？我们需要一个对标物——隐含波动率，Black-Schole公式对真实价格的解。
隐含波动率
理论上，我们应该将真实的标的物市场价格和其他四个变量带入BS方程中，来解出波动率的精确解——隐含波动率。但是由于BS方程过于负责，此法几乎不可能。
于是，我们利用数值分析方法——牛顿法，在可接受的误差范围（10^-5）内，求出BS方程的根，即隐含波动率。
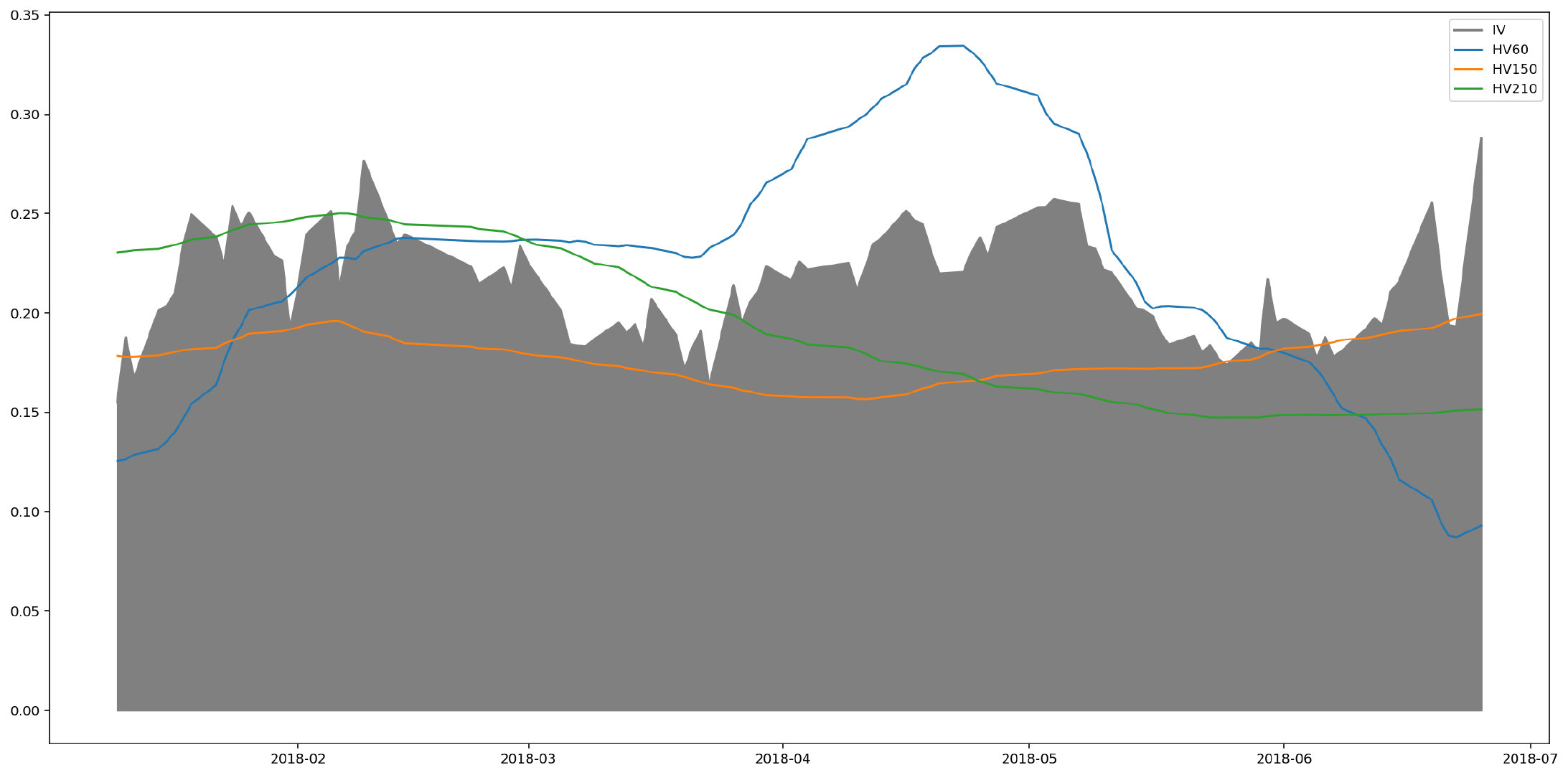如上图，我们对比了60、150、210天的历史波动率和隐含波动率，由图可直观看出60天的历史波动率过于波动，而210天的波动率过于平稳并且波动方向过于迟缓，150天的历史波动率拟合较好。
计算三不同波动率分别与隐含波动率的平均百分比绝对误差，如下图。
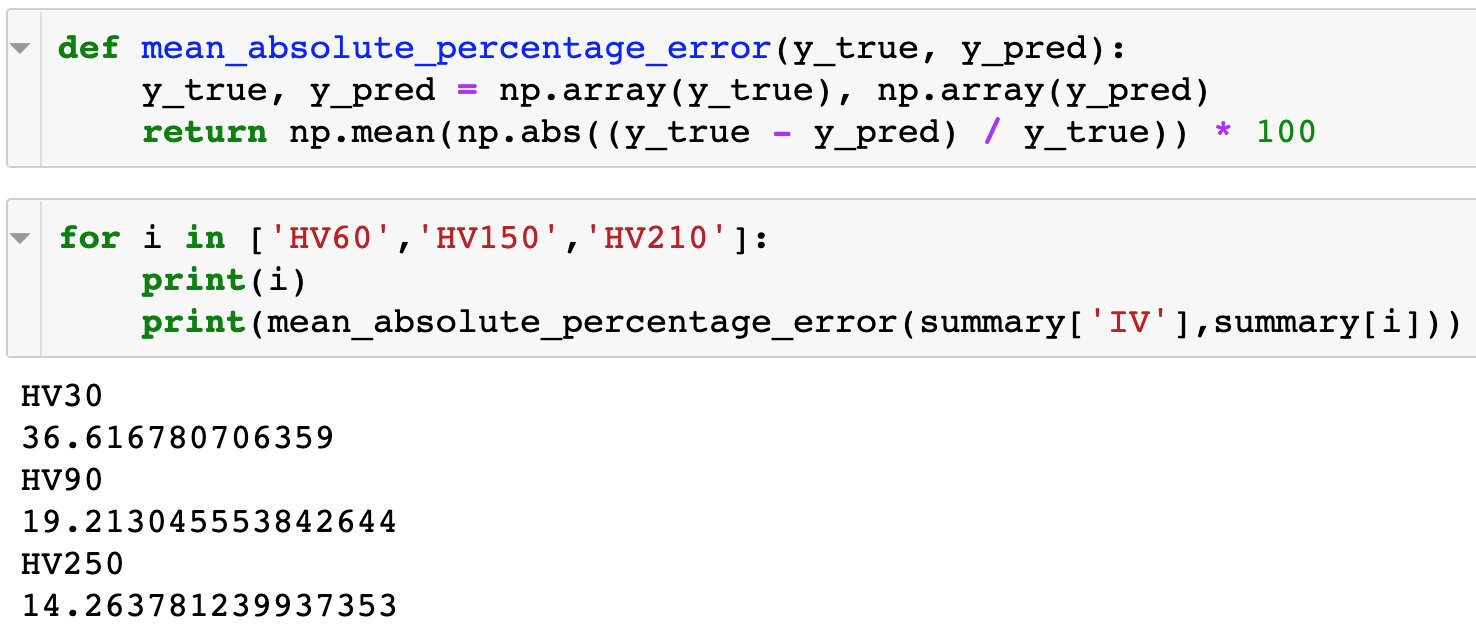
150天的历史波动率平均百分比绝对误差最低。
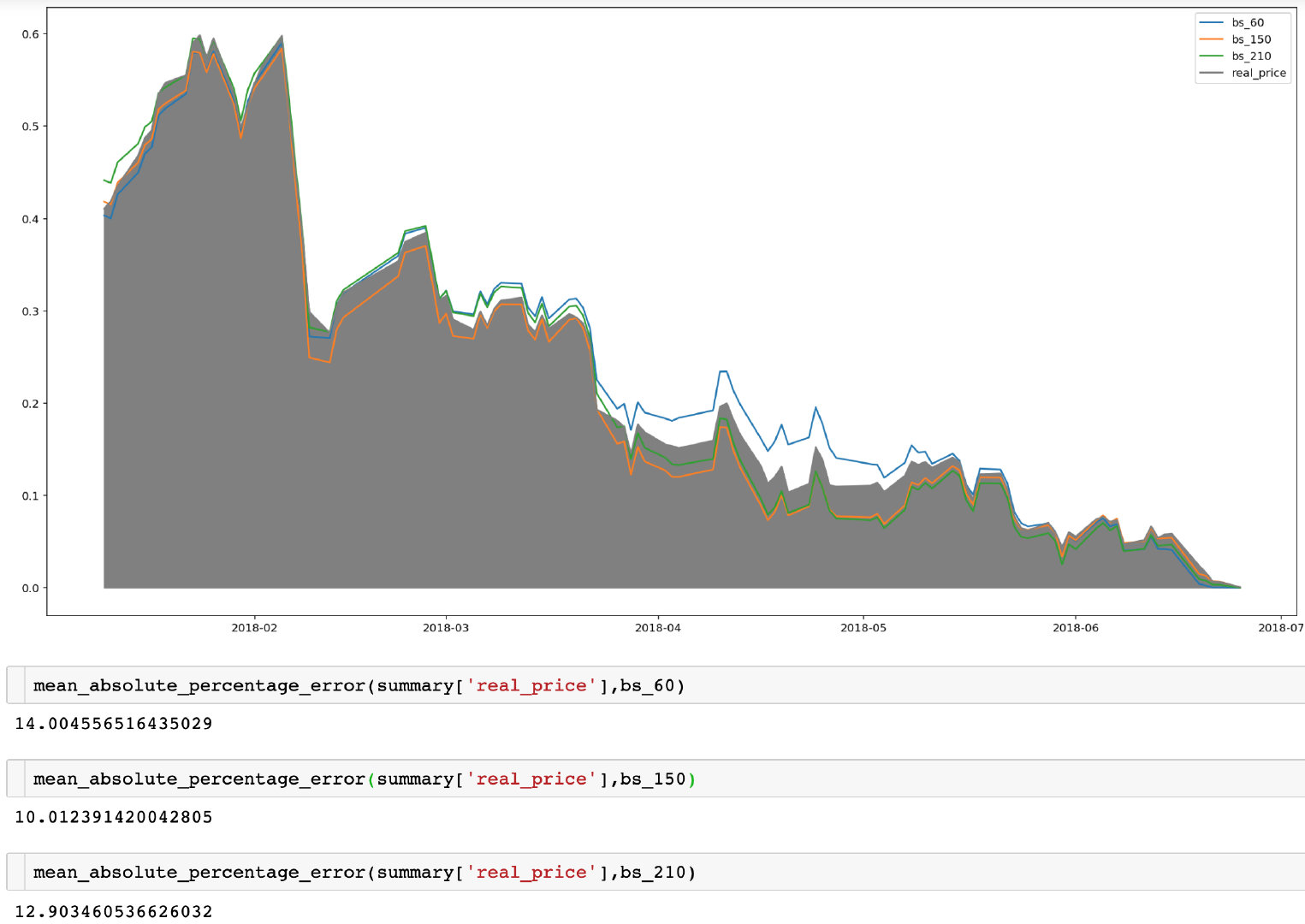
如上图，将三不同的历史波动率带入BS模型求的模拟值和真实值做对比。
图中可以较明显的看出150天历史波动率模拟出来的价值比较接近灰色的真实价格；并且三个模拟值和真实值的平均百分比绝对误差也是150天的最低。
Exponential Weighted Moving Average
对于历史波动率来说，过去的天数对于所说要求的当天波动率来说重要性是一样的，昨天和前天一样重要。
如果给过去的数据重要性加一个权重，使t-1的数据对t数据很重要，t-2次之，t-3再次之，以此类推。这即是EWMA的思想。
权重 \(\lambda= \frac{N-1}{N+1}\)
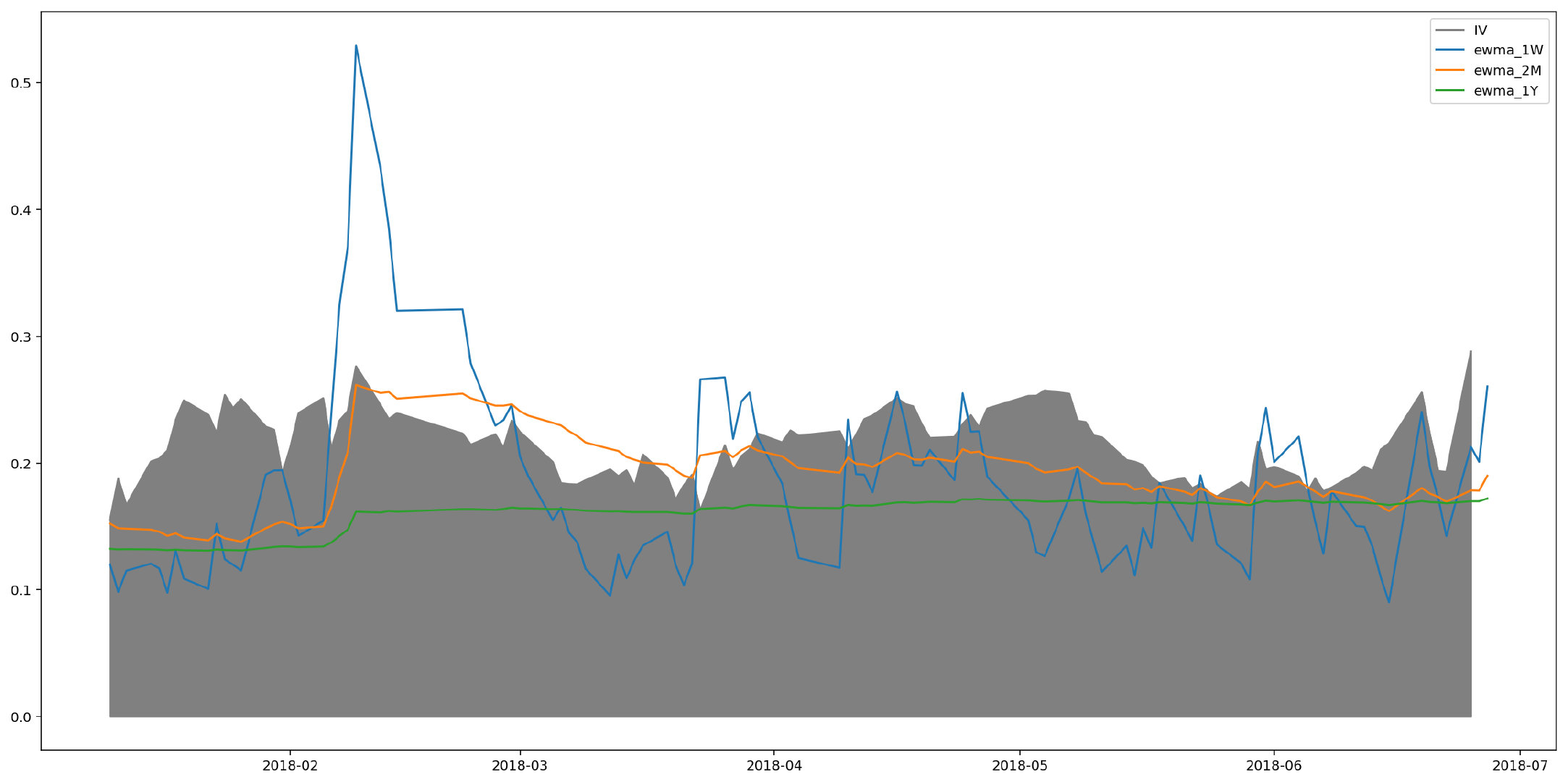
如图，作出时长分别是1周、1个月和5个月的EWMA拟合的波动率与隐含波动率的对比图。
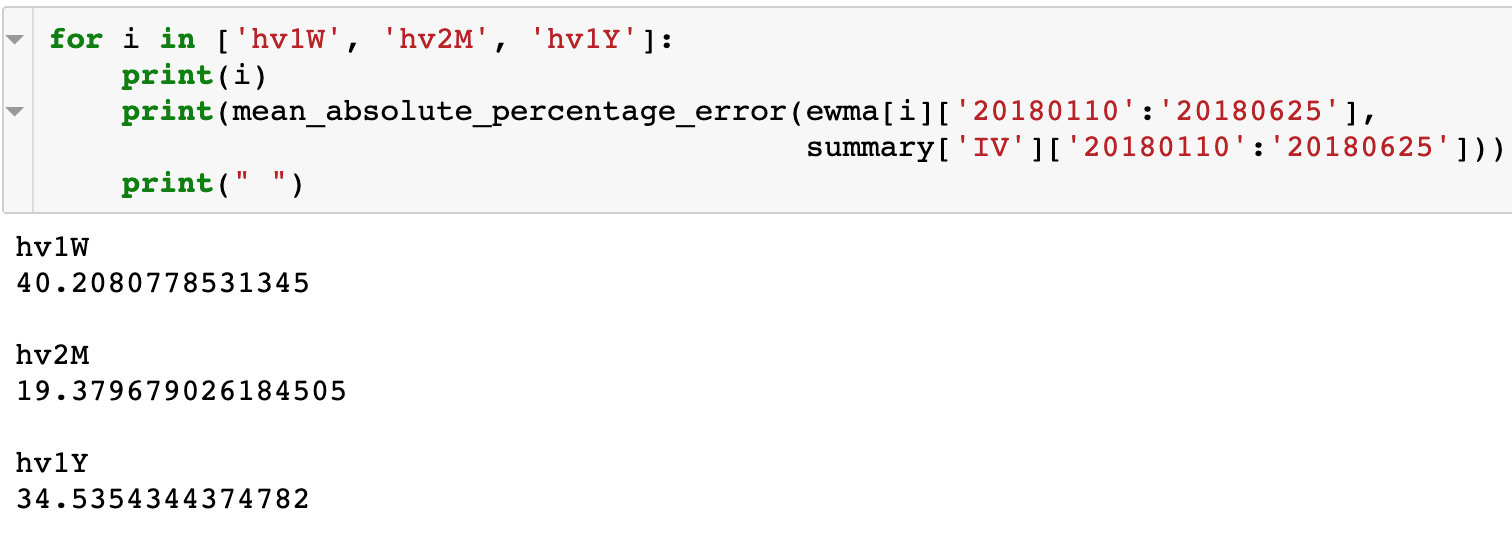
如上图，计算不同时长的EWMA与隐含波动率的平均百分比绝对误差。
GARCH(1,1)
GARCH(1,1)与EWMA不同的地方在于，GARCH多了一个常数参数项。GARCH的假设认为，波动率是有粘性的(persistence)，过去的强（若）波动会延续到未来，所以多出的常数参数项使其具有类似”均值回归”的特性。
GARCH模型建立
输出的结果如下，且Convariance estimator显示是robust。
AR - GARCH Model Results
| Dep. Variable: | y | R-squared: | 0.045 |
|---|---|---|---|
| Mean Model: | AR | Adj. R-squared: | -0.051 |
| Vol Model: | GARCH | Log-Likelihood: | 66.8673 |
| Distribution: | Normal | AIC: | -109.735 |
| Method: | Maximum Likelihood | BIC: | -79.8710 |
| No. Observations: | 89 | ||
| Date: | Wed, Apr 10 2019 | Df Residuals: | 77 |
| Time: | 03:44:24 | Df Model: | 12 |
Mean Model
| coef | std err | t | P>|t| | 95.0% Conf. Int. | |
|---|---|---|---|---|---|
| Const | -0.0307 | 1.124e-02 | -2.733 | 6.269e-03 | [-5.274e-02,-8.691e-03] |
| y[1] | 0.1976 | 0.125 | 1.577 | 0.115 | [-4.801e-02, 0.443] |
| y[2] | -0.2210 | 0.123 | -1.802 | 7.157e-02 | [ -0.461,1.940e-02] |
| y[3] | 0.1046 | 0.141 | 0.740 | 0.460 | [ -0.173, 0.382] |
| y[4] | -0.2671 | 0.145 | -1.847 | 6.476e-02 | [ -0.551,1.635e-02] |
| y[5] | -0.0467 | 0.123 | -0.381 | 0.703 | [ -0.287, 0.193] |
| y[6] | -0.1292 | 0.140 | -0.926 | 0.354 | [ -0.403, 0.144] |
| y[7] | -0.0406 | 0.146 | -0.279 | 0.780 | [ -0.326, 0.245] |
| y[8] | 0.0537 | 0.135 | 0.398 | 0.691 | [ -0.211, 0.318] |
Volatility Model
| coef | std err | t | P>|t| | 95.0% Conf. Int. | |
|---|---|---|---|---|---|
| omega | 2.4885e-04 | 5.620e-04 | 0.443 | 0.658 | [-8.526e-04,1.350e-03] |
| alpha[1] | 0.0604 | 4.475e-02 | 1.351 | 0.177 | [-2.727e-02, 0.148] |
| beta[1] | 0.9396 | 6.462e-02 | 14.539 | 6.873e-48 | [ 0.813, 1.066] |
由上表参数可得GARCH公式：
\(\sigma_{t}^{2} = 0.000280 +0.075702\alpha_{t-1}^{2} + 0.924298\sigma_{t-1}^{2}\)
\(r_{t} = -0.0307+0.1976a_{t-1} -0.2210a_{t-2} +0.1046a_{t-3}-0.2671a_{t-4}-0.0467a_{t-5} -0.1292a_{t-6}-0.0406a_{t-7}+0.0537a_{t-8}\)
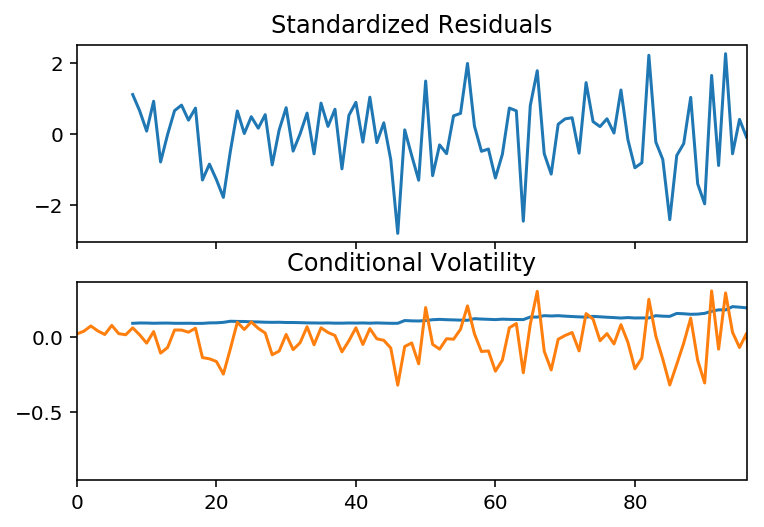
观察上图，第一张图为标准化残差，近似平稳序列，说明模型在一定程度上是正确的；
第二张图，黄色为原始收益率序列、蓝色为条件异方差序列，可以发现条件异方差很好得表现出了波动率。
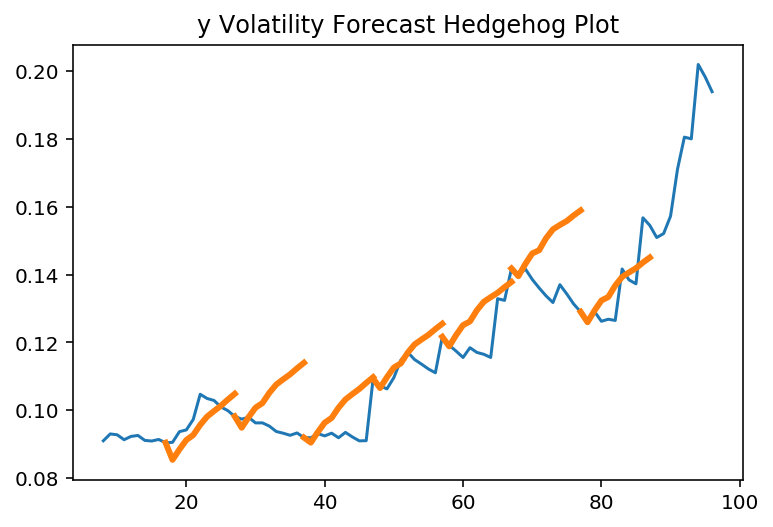
观察上图的拟合图发现，在方差的还原上还是不错的。
波动率预测
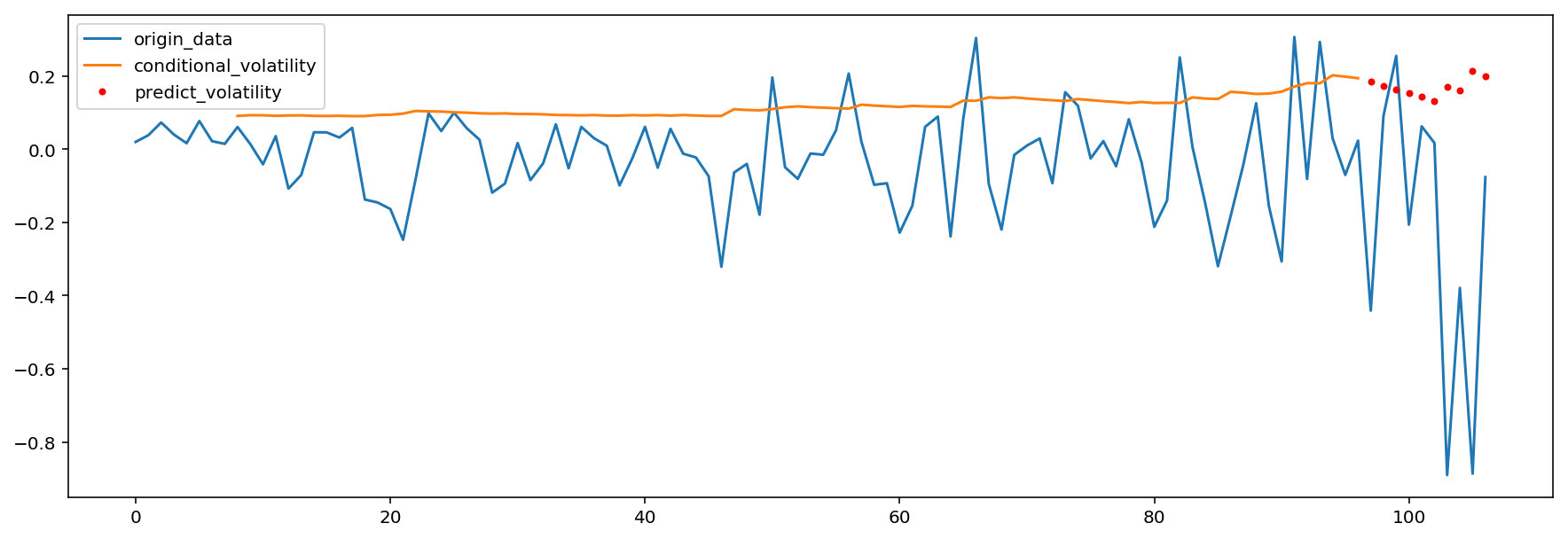
观察上述预测图发现，对于接下来的1、2天的波动率预测较为接近，然后后面几天的预测逐渐偏小，最后一两天又逐渐符合现实波动率。
